C++助教问题汇总2
周四实验课遇到的高频编程问题,简单汇总了一下。
随机数生成为什么要初始化种子
同学们看起来有两个疑惑:
- 为什么我要初始化种子?
- 为什么我又不能每次都初始化种子?
这要从(伪)随机数的原理,线性同余算法讲起。我先用一个简单的例子引入:
线性同余算法
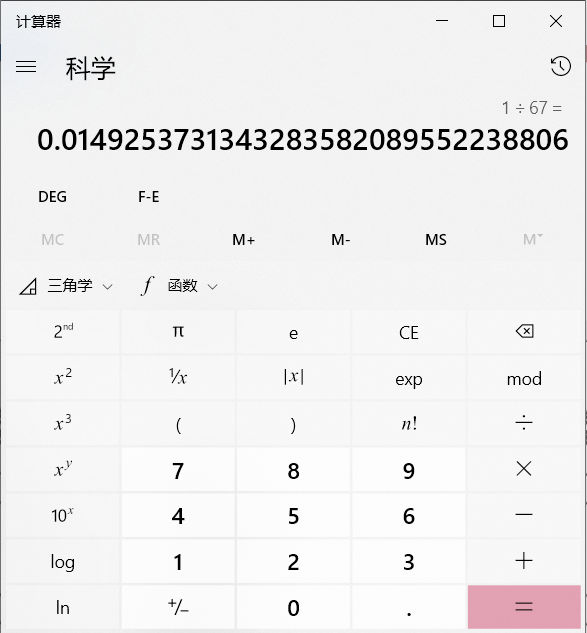
1÷67的小数部分,看起来特别没有规律。
如果我每次截取小数点后面的3个数字,我们将得到:014,925,373,134,328,……。
看,如果我不告诉你这些数字的产生原理,是不是看起来我就像拥有了一个0~999的随机数发生器?
线性同余算法 (Linear congruential generator) 正是基于类似的原理。
照搬百度百科上的定义,设 $X_n$ 是产生的第 $n$ 的(伪)随机数,$a, b, c$ 为固定整数参数,则线性同余发生器(LCG)的定义如下,
$$
X_{n+1} = (a X_{n} + c) \ \rm{mod} \ m
$$
通过选取不同的参数 $a, b, c$, 这个伪随机序列 ${ X_n }$ 可以任意变换。如果你只能观测这个序列已产生的部分,不知道它的参数,也是不可能预测这个序列之后的部分的。
当然,线性同余算法也有缺陷,就是这个序列一定有周期,不过只要周期足够大,就可以不考虑这个问题。
随机种子 (Random Seed)
为了确保线性同余序列的周期足够大,或者说这个参数的质量足够优良,通常 $a$, $b$ 和 $m$ 是数学家找好以后写死在代码里的。下面是一个线性同余生成器的实现,其中$a=214013$, $b=2531011$, $m=32768$(截取的不是尾部1-15位,而是31到16位,略有差异无妨)。
1 | |
运行结果是
1 | |
但是,这个程序每次运行时给出的结果都是一样的。毕竟,运算方式都是固定在里面的,而初值也一直都是0。
因此,我们引入随机数种子的概念。它其实就是用不同的值对_next进行初始化,相当于在这个周期超长的伪随机序列上选取不同的起点。
1 | |
运行结果是
1 | |
现在告诉你,这份代码是对Windows上的C++随机数内部实现的严格复现(源代码写得更绕一些)。将my_srand()和my_rand()换为srand()和rand(),结果将是完全一致的(请动手试一试)!
是不是,原理也没那么复杂?
何时重置种子
回到那个问题
- 为什么我要初始化种子?
- 为什么我又不能每次都初始化种子?
线性同余生成器确保了每次调用rand()时总在一个伪随机序列环上取数,上一个数和下一个数看之间看不出关联性,但每次程序运行时都从该环的同一个位置开始行走,每次都将输出相同的随机数序列。因此,用时间作为种子,可以使得不同时间运行的同一份程序从该环的不同位置上开始行走。然而,如果在每次取随机数时都用时间赋种子,则随机数生成器退化成报时器。
感谢W的屁股蛋子!
封面来自小日子老师@Liduke的微博。