凸优化实战2

今天让我们挑战一个颇有难度的优化问题, Rank-SVM ……

Rank-SVM ^[2] 是2001年提出的一个多标签学习模型，它在 SVM 的结构下，通过最小化一个类似于 Ranking Loss 的损失函数来实现多标签预测.

从 soft-SVM 开始

为了便于读者理解，我们先从一般性的 SVM 推导开始。

问题定义

一般的 soft-SVM 由如下优化问题定义

$$
\begin{equation}
\begin{aligned}
\min_{w} \quad &
\frac{1}{2} \|w\|^2 +
C \sum_{i} \xi_{i} \\
s.t. \quad &
y_i (x_{i}^T w) \geq 1 - \xi_{i} \\
\quad &
\xi_{i} \geq 0
\end{aligned}
\end{equation}
$$

对偶问题求解

为了解上述问题，我们先求拉格朗日函数

$$
\begin{equation}
\begin{aligned}
\mathcal{L}(w, \xi, \alpha, \beta) = \quad &
\frac{1}{2} \|w\|^2 + C \sum_{i} \xi_{i} + \\
\quad &
\sum_i \alpha_i (1 - \xi_{i} - y_i (x_{i}^T w)) +
\sum_i \beta_i (- \xi_{i})
\end{aligned}
\end{equation}
$$

对偶问题

$$
\begin{equation}
\begin{aligned}
\max_{\alpha, \beta} \quad &
\left(\min_{w, \xi} \ \mathcal{L}(w, \xi, \alpha, \beta) \right) \\
s.t. \quad &
\alpha_i \geq 0 \\
\quad &
\beta_i \geq 0
\end{aligned}
\end{equation}
$$

对拉格朗日函数关于 $w$ 和 $\xi$ 最小化

$$
\begin{equation}
\frac{\partial}{\partial \xi_i} \mathcal{L} = 0 \Rightarrow \alpha_i + \beta_i = C
\end{equation}
$$

$$
\begin{equation}
\frac{\partial}{\partial w} \mathcal{L} = 0 \Rightarrow w = \sum_{i} \alpha_i y_i x_i
\end{equation}
$$

代入后可以暂做一部分化简，消去 $w, \xi$,

对于形如 $\frac{1}{2} x^T x + (\dots)^T x$ 的式子, 显然其最小值为 $-\frac{1}{2} x^2$.

$$
\begin{equation}
\begin{aligned}
\max_{w, \xi} \mathcal{L}(w, \xi, \alpha, \beta) = \quad &
\frac{1}{2} \|w\|^2 - \bigl( \sum_i \alpha_i y_i x_i \bigr)^T w \ + \\
\quad &
\sum_i \alpha_i + \sum_i (C - \alpha_i - \beta_i) \xi_i \\
= \quad &
-\frac{1}{2} \|w\|^2 + \sum_i \alpha_i \\
= \quad & -\frac{1}{2} \alpha^T Z \alpha + \vec{1}^T \alpha
\end{aligned}
\end{equation}
$$

顺便连 $\beta$ 也消掉了,
其中为简便运算，定义了 $z_{ij} = y_i y_j \langle x_i, x_j \rangle$, 即

$$
\begin{equation}
Z = Y Y^T \odot X X^T
\end{equation}
$$

再求关于 $\alpha$ 的最小化

$$
\begin{equation}
\begin{aligned}
\min_{\alpha} \quad &
\frac{1}{2} \alpha^T Z \alpha - \vec{1}^T \alpha \\
s.t. \quad &
0 \leq \alpha_i \leq C
\end{aligned}
\end{equation}
$$

可以看出是很明显的关于 $\alpha$ 的正定二次规划问题.
用投影梯度下降 (Projected Gradient Descent) 的方法可以非常简单地求解，例如

$$
\alpha \leftarrow \max \bigl(0, \min \bigl(C, \alpha -\eta (Z \alpha - \vec{1}) \bigr) \bigr)
$$

其中 $\eta$ 是优化步长，最后代入 $w = \sum_i \alpha_i y_i x_i$ 即可.

数值求解

对于无约束的二次规划问题，可以采用 共轭梯度下降法, BFGS算法 或者 L-BFGS算法，它们都只使用一阶导数信息。

为了处理正空间约束，可以采用梯度投影法 (Gradient Projection Method).

Rank-SVM

问题定义

原论文 ^{[1] [2]} 中对该问题的定义如下

问题定义为

$$
\begin{equation}
\begin{aligned}
\min_{W} \quad &
\frac{1}{2} \|W\|^2_F +
\sum_{i=1}^{n} \lambda_i
\sum_{p \in \mathcal{Y}_i} \sum_{q \in \bar{\mathcal{Y}}_i} \xi_{ipq} \\
s.t. \quad &
x_i^T(w_p - w_q) \geq 1 - \xi_{ipq},
\quad (p,q) \in \mathcal{Y}_i \times \bar{\mathcal{Y}}_i \\
\quad &
\xi_{ipq} \geq 0
\end{aligned}
\end{equation}
$$

其中, $\lambda_i = \lambda_{ipq} = \frac{C}{|\mathcal{Y}_i||\bar{\mathcal{Y}}_i|}$.

对偶问题

为简便起见，我们约定几个下表字母.
当 $i$ 作为下标时，始终表示 $i \in \{1, \dots, n\}$,
以此类推,
$j \in \{1, \dots, m\}$,
$k \in \{1, \dots, q\}$,
$p \in \mathcal{Y}_i$,
$q \in \bar{\mathcal{Y}}_i$.

尽管这样可以获得叙述上的方便，但我们还是要时刻注意 $p,q$ 的取值依赖于 $i$.

采用类似 Soft-SVM 的技巧，求拉格朗日函数

$$
\begin{equation}
\begin{aligned}
\mathcal{L}(w, \xi, \alpha, \beta) = \quad &
\frac{1}{2} \|W\|^2_F +
C \sum_{i,p,q} \lambda_i \xi_{ipq} + \\
\quad &
\sum_{i,p,q} \alpha_{ipq} (1 - \xi_{ipq} - x_i^T (w_p - w_q)) + \\
\quad &
\sum_{i,p,q} \beta_{ipq} (-\xi_{ipq})
\end{aligned}
\end{equation}
$$

对偶问题

$$
\begin{equation}
\begin{aligned}
\max_{\alpha, \beta} \quad &
\left(\min_{w, \xi} \ \mathcal{L}(w, \xi, \alpha, \beta) \right) \\
s.t. \quad &
\alpha_{ijk} \geq 0 \\
\quad &
\beta_{ijk} \geq 0
\end{aligned}
\end{equation}
$$

对拉格朗日函数关于 $w$ 和 $\xi$ 最小化

$$
\begin{equation}
\frac{\partial}{\partial \xi_{ipq}} \mathcal{L} = 0 \Rightarrow
\alpha_{ipq} + \beta_{ipq} = \lambda_i
\end{equation}
$$

$$
\begin{equation}
\begin{aligned}
\frac{\partial}{\partial w_{jk}} \mathcal{L} = 0 \Rightarrow
w_{jk} & =
\sum_{i, \ \rm{if} \ k \in \bar{\mathcal{Y}}_i}
x_{ij} \sum_{p \in \mathcal{Y}_i} \alpha_{ipk} -
\sum_{i, \ \rm{if} \ k \in \mathcal{Y}_i}
x_{ij} \sum_{q \in \bar{\mathcal{Y}}_i} \alpha_{ikq} \\
& =
\sum_{i,l} \left(
y_{ik} (1-y_{il}) \alpha_{ikl} -
y_{il} (1-y_{ik}) \alpha_{ilk}
\right) x_{ij} \\
& =
\sum_{i,l} \left(
\tilde y_{ikl} \alpha_{ikl} -
\tilde y_{ilk} \alpha_{ilk}
\right) x_{ij} \\
& =
\sum_{i,l,r}
\tilde y_{ilr} (
[l=k] - [r=k]
) \alpha_{ilr} x_{ij} \\
& =
\sum_{i,l,r}
\tilde y_{ilr} c_{klr} \alpha_{ilr} x_{ij} \\
& =
\sum_{i,p,q}
c_{kpq} \alpha_{ipq} x_{ij}
\end{aligned}
\end{equation}
$$

其中

$$
\begin{equation}
\begin{aligned}
\tilde y_{ipq} = \ &
y_{ip} (1 - y_{iq}) \\
= \ &
\left\{ \begin{aligned}
1, \quad &
p \in \mathcal{Y}_i \ \mathrm{and} \
q \in \bar{\mathcal{Y}}_i \\
0, \quad &
\mathrm{else} \\
\end{aligned} \right.
\end{aligned}
\end{equation}
$$

$$
\begin{equation}
\begin{aligned}
c_{kpq} = \ &
[p=k] - [q=k] \\
= \ &
\left\{ \begin{aligned}
1, \quad &
p=k \ \mathrm{and} \ q \neq k \ \\
-1, \quad &
p \neq k \ \mathrm{and} \ q = k \ \\
0, \quad &
\mathrm{else} \\
\end{aligned} \right.
\end{aligned}
\end{equation}
$$

对 $\|w\|_F^2$ 进行化简

$$
\begin{equation}
\label{eq:w2}
\begin{aligned}
\|w\|_F^2 & = \
\sum_{j,k} w_{jk}^2 \\
& = \
\sum_{i,p,q,i^{\prime},p^{\prime},q^{\prime},j,k}
c_{kpq} \ c_{kp^{\prime}q^{\prime}} \
x_{ij} \ x_{i^{\prime}j} \
\alpha_{ipq} \ \alpha_{i^{\prime}p^{\prime}q^{\prime}} \\
\end{aligned}
\end{equation}
$$

向量化

注意到 $p,q$, 以及 $p^{\prime},q^{\prime}$ 总是成对出现，
由于我们总是可以将整数对 $(p,q)$ 映射到另一个正整数 $\mu$ 上，为了叙述上的简便我们用 $\mu$ 代替 $(p,q)$.

这样，$\alpha_{ipq}$ 可以表示为 $\alpha_{i\mu}$.
这可以视为对张量隐式的向量化(Vectorization)。

上式继续化简为

$$
\begin{equation}
\begin{aligned}
\|w\|_F^2 & = \
\sum_{i,\mu,i^{\prime},\mu^{\prime},j,k}
c_{k\mu} \ c_{k\mu^{\prime}} \
x_{ij} \ x_{i^{\prime}j} \
\alpha_{i\mu} \ \alpha_{i^{\prime}\mu^{\prime}} \\
& = \
\sum_{i,\mu,i^{\prime},\mu^{\prime}}
\langle c_{\bullet \mu},\ c_{\bullet \mu^{\prime}} \rangle \
\langle x_{i \bullet} \ x_{i^{\prime} \bullet} \rangle \
\alpha_{i\mu} \ \alpha_{i^{\prime}\mu^{\prime}} \\
& = \
\mathrm{vec}(\alpha)^T A \ \mathrm{vec}(\alpha)
\end{aligned}
\end{equation}
$$

其中 $\mathrm{vec}(\bullet)$ 为对矩阵的向量化, $\otimes$ 为克罗内克积 (Kronecker Product).
$A$ 定义为

$$
A = X X^T \otimes C^T C
$$

由向量化和克罗内克积定义，有

$$
\mathrm{vec}(\alpha)_{(i\mu)} = \alpha_{i\mu}
$$

且

$$
a_{(i\mu)(i^{\prime} \mu^{\prime})}
= (X X^T)_{i i^{\prime}} (C^T C)_{\mu \mu^{\prime}}
= \langle x_{i \bullet} \ x_{i^{\prime} \bullet} \rangle \
\langle c_{\bullet \mu},\ c_{\bullet \mu^{\prime}} \rangle
$$

代入化简，消去 $w, \xi$, 得到最终的对偶问题

$$
\begin{equation}
\begin{aligned}
\min_{\alpha} \mathcal{L}(\alpha) \quad & =
\frac{1}{2}\sum_{j,k} w_{jk}^2 - \sum_{i,p,q} \alpha_{ipq} \\
\quad & =
\mathrm{vec}(\alpha)^T A \ \mathrm{vec}(\alpha) -
\vec{1}^T \mathrm{vec}(\alpha) \\
s.t. \quad &
0 \leq \alpha_{ipq} \leq \lambda_i
\end{aligned}
\end{equation}
$$

可以看到我们最终还是将其化为了一个凸正定锥二次规划问题.

我们总算把这个伟大的化简做完了！

稀疏矩阵密集化

该问题规模为 $n q^2$, 其中系数矩阵 $A \in \mathbb{R}^{n q^2 \times n q^2}$. 对于中等规模及以上，或者标签数量偏多的数据集，求解该问题所需的空间开销不可接受. 这要求我们继续讨论如何避免不必要的开销.

在上述推导过程中，我们通过约定 $p, q$ 总满足 $p \in \mathcal{Y}_i, q \in \bar{\mathcal{Y}}_i$, 以此忽略了 $\tilde y$ 项的计算, 不严谨地得到了上述结果.

事实上，$a_{(i\mu)(i^{\prime} \mu^{\prime})}$ 应该为

$$
a_{(i\mu)(i^{\prime} \mu^{\prime})}
= \langle x_{i \bullet} \ x_{i^{\prime} \bullet} \rangle \
\langle c_{\bullet \mu},\ c_{\bullet \mu^{\prime}} \rangle \
\tilde{y}_{i\mu} \ \tilde{y}_{i^{\prime}\mu^{\prime}}
$$

或者说，把对 $A$ 的修正项外提，最终得到的对偶问题形式应当为

$$
\begin{equation}
\begin{aligned}
\min_{\alpha} \mathcal{L}(\alpha) \quad & =
\mathrm{vec}(\tilde{y} \odot \alpha)^T A \ \mathrm{vec}(\tilde{y} \odot \alpha) -
\vec{1}^T \mathrm{vec}(\tilde{y} \odot \alpha) \\
s.t. \quad &
\mathrm{vec}(\tilde{y} \odot \alpha) \geq \vec{0}
\end{aligned}
\end{equation}
$$

即，对于 $\alpha$, 仅 $\tilde{y}_{ipq} = 1$ 时 $\alpha_{ipq}$ 参与计算且有意义. 换言之 $\alpha$ 本身就是稀疏的，我们真正希望优化的部分是 $\tilde{y} \odot \alpha$.

因此，我们可以定义一个新的密集化函数 $\mathrm{dense}(\vec{a}, \vec{b})$ , 该函数丢弃 $a$ 中所有 $b_i$ 为0位置上的元素，将其余元素拼接为新的向量. 我们记 $\tilde{\alpha} = \mathrm{dense}(\mathrm{vec}(\alpha), \mathrm{vec}(\tilde y))$,

因此对偶问题变为

$$
\begin{equation}
\begin{aligned}
\min_{\tilde{\alpha}} \mathcal{L}(\tilde{\alpha}) \quad &
\tilde{\alpha}^T \tilde{A} \ \tilde{\alpha} -
\vec{1}^T \tilde{\alpha} \\
s.t. \quad &
0 \leq \tilde{\alpha} \leq \tilde{\lambda}
\end{aligned}
\end{equation}
$$

其中 $\tilde{\lambda} = \mathrm{dense}(\mathrm{vec}(\lambda))$, $\tilde{A}$ 为我们删除掉 $A$ 中不关心的行列后得到的密集矩阵. 如果把矩阵看作以列向量为元素的向量，那么也可以用比较绕的方式这么定义 $\tilde{A}$,

$$
\begin{equation}
\tilde{A} = \mathrm{dense}(
\mathrm{dense}(
A^T,
\mathrm{vec}(\tilde y)
)^T,
\mathrm{vec}(\tilde y)
)
\end{equation}
$$

尽管规模较小的 $\tilde{A}$ 便利了后续优化求解的效率，但 $A$ 的中间计算不可避免，空间开销依然庞大，对于中等规模及以上的问题均难以接受.

可以作为优化问题推导的练手，但就方法本身非常过时.

附言: 原论文的推导

如果你去读原论文^[1]，会发现其求解方法和我们的前半段相似，后半段不一样。

这是因为原论文没有勇气把 $\frac{\partial \mathcal{L}}{\partial w} = 0$ 得到的等式代入 $\|w\|_F^2$ 项进行化简，因此对偶问题还保留了等式约束.

此外，它也没有把 $A \in \mathbb{R}^{n q^2 \times n q^2}$ 显式地求出来, 而是在求 $\nabla \mathcal{L}(\alpha)$ 直接计算 $A \cdot \mathrm{vec}(\alpha)$，相当于放弃了向量并行化的优势，用时间换了空间. 对于 $A = X X^T \otimes C^T C$, 欲求 $A \cdot \mathrm{vec}(\alpha)$, 通过

$$
(A \cdot \mathrm{vec}(\alpha))_{(i\mu)} =
\left( (X X^T)_{i \bullet} \otimes (C^T C)_{\mu \bullet} \right)^T
\mathrm{vec}(\alpha)
$$

求 $A$ 的每个元素，这样就节省了中间变量 $A$ 原本所需的空间. 空间开销停留在 $O(n q^2)$.

代码实现

你可以在这里下载我们的示例代码

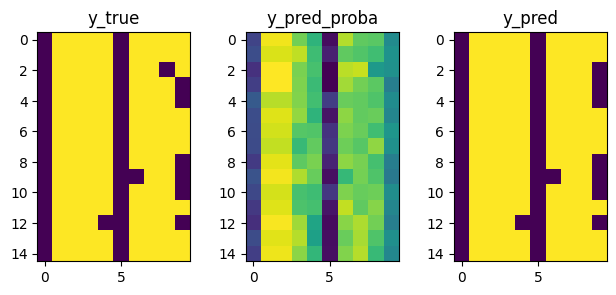
预测

引用

• [1] Elisseeff, André and Jason Weston. “Kernel methods for Multi-labelled classification and Categorical regression problems.” NIPS 2001 (2001).
• [2] Elisseeff, André, and Jason Weston. “A kernel method for multi-labelled classification.” Advances in neural information processing systems 14 (2001).

^[1][2] 是同一篇文章，^[2] 是见刊版本, ^[1] 附带了更详尽的推导，建议阅读 ^[1] 但引用 ^[2].

---

感谢 The Type 对字体文化的关注！
封面来自 The Type 的 城市字体观察：招牌备忘录。